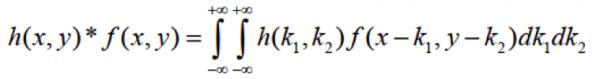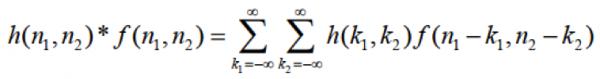Phát hiện biên của ảnh là một trong những nhiệm vụ quan trọng trong xử lý ảnh. Nhận dạng ảnh dùng máy tính liên quan tới việc nhận dạng và phân loại các đối tượng trong bức ảnh do đó phát hiện biên là một công cụ quan trọng. Phát hiện biên sẽ làm giảm một cách đáng kể khối lượng dữ liệu cần xử lý và loại bỏ các thông tin không cần thiết trong khi vẫn đảm bảo các thuộc tính quan trọng về cấu trúc của ảnh. Trong bài viết này, tìm hiểu về một số kiểu đường biên, một số kỹ thuật phát hiện biên hiện đang được sử dụng.
1. Phát hiện biên là gì?
Phát hiện biên là một công cụ quan trọng trong xử lý ảnh số. Nó làm giảm một cách đáng kể khối lượng dữ liệu cần tính toán, chỉ giữ lại một số ít những thông tin cần thiết đồng thời vẫn bảo toàn được những cấu trúc quan trọng trong bức ảnh. Trong phát hiện biên dùng mathematical morphology được so sánh với một số phương pháp phát hiện biên. Độ nhạy của các phương pháp phát hiện biên đối với tác động của nhiễu được so sánh. Phát hiện biên bằng thông qua việc xử lý các pixels dùng các ma trận, đạo hàm riêng. Trong bài viết này trình bày một số phương pháp phát hiện biên đang được sử dụng phổ biến hiện nay thông qua matlab toolbox và viết chương trình trên MATLAB 7.0 để tiến hành so sánh cả về định tính và định lượng.
2. Một số kiểu đường biên
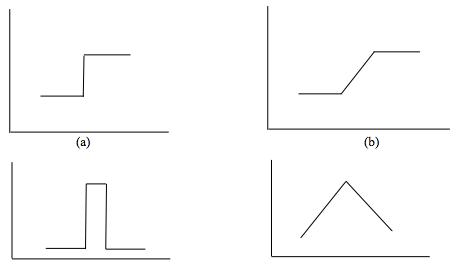
Đường biên là nơi mà các điểm ảnh lân cận nhau có cường độ thay đổi mạnh một cách đột ngột. Một số kiểu đường biên hay gặp trên thực tế được minh họa trên hình 1
Hình 1. Một số kiểu đường biên thông dụng
(a): Biên dạng nhảy bậc
(b): Biên dốc
(c): Biên dạng xung vuông
(d): Biên dạng hình nón
3. Các phương pháp phát hiện biên
Các phương pháp phát hiện biên truyền thống thường dựa trên kết quả của phép tích hập (convolution) giữa bức ảnh cần nghiên cứu f(x,y) và một bộ lọc 2D (filter) h(x,y) thường được gọi là mặt nạ (mask).
Nếu h(x,y) và f(x,y) có dạng rời rạc thì công thức trên sẽ được viết lại thành:
Trên thực tế người ta hay dùng h(n1,n2) là ma trận [3×3 ] như sau:
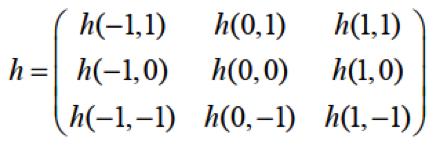
Cấu trúc và giá trị của các toán tử phát hiện biên sẽ xác định hướng đặc trưng mà toán tử nhạy cảm với biên. Có một số toán tử thích hợp cho các đường biên có hướng nằm ngang, một số toán tử lại thích hợp cho việc tìm kiếm biên dạng thẳng đứng hay theo hướng đường chéo. Có nhiều phương pháp phát hiện biên đang được áp dụng, tuy nhiên ta có thể phân thành hai nhóm cơ bản là phát hiện biên dùng Gradient và phương pháp Laplacian. Phương pháp phát hiện biên dùng Gradient (sử dụng các toán tử Roberts, Prewitt, Sobel, Canny) dựa vào tính giá trị cực đại và cực tiểu của đạo hàm bậc
nhất của ảnh. Phương pháp Laplacian sẽ tìm kiếm những điểm có giá trị 0 khi lấy đạo hàm bậc hai của ảnh.
3.1. Phương pháp Gradient
Đạo hàm bậc nhất theo hướng ngang và dọc được tính theo công thức:
Biên độ của gradient vector hay độ lớn tổng cộng của giá trị đạo hàm nằm tại biên là kết hợp của cả hai giá trị này theo công thức:
Hướng của gradient vector được xác định theo công thức:
Hướng của biên sẽ vuông góc với hướng của gradient vector này.
a. Toán tử Sobel
Trên thực tế Sobel sử dụng hai mặt nạ có kích thước [3 x 3] trong đó một mặt nạ chỉ đơn giản là sự quay của mặt nạ kia đi một góc 900. Các mặt nạ này được thiết kế để tìm ra các đường biên theo chiều đứng và chiều ngang một cách tốt nhất. Khi thực hiện phép convolution giữa ảnh và các mặt nạ này ta nhận được các gradient theo chiều đứng và chiều ngang Gx, Gy. Toán tử Sobel có dạng như hình 2.
|
-1 |
-2 |
-1 |
|
-1 |
0 |
1 |
|
0 |
0 |
0 |
|
-2 |
0 |
2 |
|
1 |
2 |
1 |
|
-1 |
0 |
1 |
Hình 2. Toán tử Sobel
b. Toán tử Prewitt
Phương pháp Prewitt gần giống với Sobel. Đây là phương pháp lâu đời nhất, cổ điển nhất. Toán tử Prewitt được mô tả trên hình 3.
|
-1 |
-1 |
-1 |
|
-1 |
0 |
1 |
|
0 |
0 |
0 |
|
-1 |
0 |
1 |
|
1 |
1 |
1 |
|
-1 |
0 |
1 |
Hình 3. Toán tử Prewitt
c. Toán tử Robert
Tương tự như Sobel, ta tính đường biên ngang và dọc một cách riêng rẽ dùng 2 mặt nạ như hình 4, sau đó tổng hợp lại để cho đường biên thực của ảnh. Tuy nhiên do mặt nạ của Robert khá nhỏ nên kết quả là bị ảnh hưởng khá nhiều của nhiễu.
|
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
-1 |
0 |
|
0 |
0 |
-1 |
|
0 |
0 |
1 |
|
0 |
1 |
0 |
Hình 4. Toán tử Robert
d. Phương pháp Canny
Phương pháp này sử dụng hai mức ngưỡng cao và thấp. Ban đầu ta dùng mức ngưỡng cao để tìm điểm bắt đầu của biên, sau đó chúng ta xác định hướng phát triển của biên dựa vào các điểm ảnh liên tiếp có giá trị lớn hơn mức ngưỡng thấp. Ta chỉ loại bỏ các điểm có giá trị nhỏ hơn mức ngưỡng thấp. Các đường biên yếu sẽ được chọn nếu chúng được liên kết với các đường biên khỏe. Phương pháp Canny bao gồm các bước sau:
Bước 1. Trước hết dùng bộ lọc Gaussian để làm mịn ảnh.
Bước 2. Sau đó tính toán gradient của đường biên của ảnh đã được làm mịn.
Bước 3. Tiếp theo là loại bỏ những điểm không phải là cực đại.
Bước 4. Bước cuối cùng là loại bỏ những giá trị nhỏ hơn mức ngưỡng.
Phương pháp này hơn hẳn các phương pháp khác do ít bị tác động của nhiễu và cho khả năng phát hiện các biên yếu. Nhược điểm của phương pháp này là nếu chọn ngưỡng quá thấp sẽ tạo ra biên không đúng, ngược lại nếu chọn ngưỡng quá cao thì nhiều thông tin quan trọng của biên sẽ bị loại bỏ. Căn cứ vào mức ngưỡng đã xác định trước, ta sẽ quyết định những điểm thuộc biên thực hoặc không thuộc biên. Nếu mức ngưỡng càng thấp, số đường biên được phát hiện càng nhiều (nhưng kèm theo là nhiễu và số các đường biên giả cũng xuất hiện càng nhiều). Ngược lại nếu ta đặt mức ngưỡng càng cao, ta có thể bị mất những đường biên mờ hoặc các đường biên sẽ bị đứt đoạn.
Phương pháp Canny có các ưu điểm sau:
- Cực đại hóa tỷ số tín hiệu trên nhiễu làm cho việc phát hiện các biên thực càng chính xác.
- Đạt được độ chính xác cao của đường biên thực.
- Làm giảm đến mức tối thiểu số các điểm nằm trên đường biên nhằm tạo ra các đường biên mỏng, rõ.
3.2. Phương pháp Laplacian of Gaussian (LOG)
Dùng phương pháp gradient sẽ cho kết quả là ảnh nhận được có cấu trúc không rõ nét do tạo nên những đường biên dày, không sắc nét. Để nhận được các đường biên mỏng và rõ nét, ta phải tiến hành các bước xử lý tiếp theo như loại bỏ những điểm không phải là cực trị (nonmaximum suppression) đồng thời áp dụng kỹ thuật liên kết biên (edge linking). Ngoài ra ta còn gặp phải vấn đề là làm thế nào để xác định được mức ngướng một cách chính xác. Việc chọn đúng giá trị ngưỡng phụ thuộc rất nhiều vào nội dung của từng bức ảnh. Nếu ta tăng gấp đôi kích thước của một bức ảnh mà không thay đổi giá trị cường độ của các điểm ảnh, ta sẽ nhận được gradients bị suy giảm đi một nửa. Mặt khác kích thước của mặt nạ (masks) cũng ảnh hưởng nhiều đến giá trị của gradients trong ảnh.
Phương pháp gradient chỉ thích hợp cho các vùng ảnh độ tương phản thay đổi có tính nhảy bậc, điều này gây khó khăn cho phát hiện các đường thẳng. Để khắc phục nhược điểm này ta thường dùng đạo hàm bậc hai. Phương pháp Laplacian cho phép xác định đường biên dựa vào giá trị 0 của đạo hàm bậc hai của ảnh.
Laplacian của một ảnh tại điểm I(x,y) được tính theo công thức:
Laplacian được kết hợp với bộ lọc làm mịn ảnh để tìm biên. Xét công thức sau:
Ở đây r2 = x2+ y2 và ơ là độ lệch chuẩn (standard deviation). Nếu thực hiện phép tích chập của hàm này với ảnh cần tìm biên, kết quả là ảnh sẽ bị mờ đi, mức độ mờ phụ thuộc vào giá trị của ơ. Laplacian của h tức đạo hàm bậc hai của h theo r là:
Hàm này thường được gọi là Laplacian of a Gaussian (LoG) có dạng Gaussian.
Trong phương pháp này, bộ lọc Gaussian được kết hợp với Laplacian cho phép hiển thị những vùng ảnh có cường độ thay đổi nhanh do đó làm tăng hiệu quả phát hiện biên. Nó cho phép làm việc với một diện tích rộng hơn xung quanh điểm ảnh đang được nghiên cứu nhằm phát hiện chính xác hơn vị trí của đường biên. Nhược điểm của phương pháp này là không xác định được hướng của biên do sử dụng hai bộ lọc Laplacian quá khác nhau có dạng như trên hình 5.
|
0 |
-1 |
0 |
|
-1 |
-1 |
-1 |
|
-1 |
4 |
-1 |
|
-1 |
8 |
-1 |
|
0 |
-1 |
0 |
|
-1 |
-1 |
-1 |
Hình 4. Toán tử Robert
Mỗi phương pháp đều có những ưu nhược điểm nhất định. Tùy thuộc vào tính chất phức tạp của nội dung trong từng bức ảnh, để tìm kiếm một phương pháp thích hợp và tối ưu nhất.
TÀI LIỆU THAM KHẢO
[1]. Beant Kaur, Anil Garg, Comparative study of different edge detection techniques, International journal of Engineering Science and Technology (IJEST), vol. 3, No. 3 March 2011.
[2] Raman Maini and Dr. Himanshu Aggarwai, Study and Comparison of various Image Edge Detection Techniques, International journal of Image Processing, Volume 3, Issue 1.
[3] Bindu Bansal, Jasbir Singh Saini, Vipan Bansal and Gurjit Kaur, “Comparison of various edge detection techniques”, Journal of Information and Operations Management, Vol 3, Issue 1, 2012, pp. 103-106.
[4] John Schmeelk, AC2011-279: “Edge Detectors in Image Processing”, American Society for Engineering Education Annual Conference and Exposition, 26-29 June 2011, Vancouver, BC, Canada,
[5] Rafael C. Gonzalez and Richard E. Woods, “Digital Image Processing”, 2nd edition, PrenticeHall,Inc, 2002.
Tin mới
- Lễ bế giảng cho sinh viên đại học chính quy khóa K8 KSXD & K9 CNTT - 27/08/2020 10:21
- Giao nhiệm vụ thực tập tốt nghiệp cho Sinh viên K9, K10 ngành kỹ thuật xây dựng - 21/08/2020 08:35
- Lễ bảo vệ Đồ án tốt nghiệp của sinh viên Ngành Kỹ thuật xây dựng đợt 2 Năm học 2019-2020 - 15/08/2020 09:18
- Chia tay tuổi học trò – đến với ngôi nhà HTU - 21/07/2020 02:47
- Khoa Kỹ thuật – Công nghệ tổ chức bảo vệ khóa luận tốt nghiệp Khóa học 2016 – 2020 - 21/07/2020 01:33
Các tin khác
- Thông tin Tuyển sinh Khoa Kỹ thuật-Công nghệ - 12/06/2020 02:04
- Lễ bảo vệ đồ án tốt nghiệp của sinh viên ngành Kỹ thuật xây dựng Khoá 2015-2020 - 25/05/2020 01:20
- Khoa Kỹ thuật công nghệ tổ chức xét duyệt thành công đề tài sinh viên nghiên cứu khoa học Năm học 2019-2020 - 07/05/2020 01:22
- Trường Đại học Hà Tĩnh – ngôi trường chắp cánh cho ước mơ của tôi - 30/04/2020 04:04
- Phần mềm ATENA trong nghiên cứu bê tông cốt thép - 20/04/2020 18:19