Là một lĩnh vực của khoa học máy tính – Đồ họa máy tính có sự phát triển nhanh chóng, giúp giao tiếp giữa con người và máy tính trở nên thân thiện. Các chương trình đồ họa ứng dụng rất phong phú và đa dạng trong tất cả các lĩnh vực.
Bài báo này đề cập đến giải thuật vẽ ngôi sao và bông hoa trên cơ sở các giải thuật vẽ hình cơ bản của đồ họa máy tính bằng ngôn ngữ Java.
NỘI DUNG
1. Vẽ ngôi sao 5 cánh
- Ý tưởng:
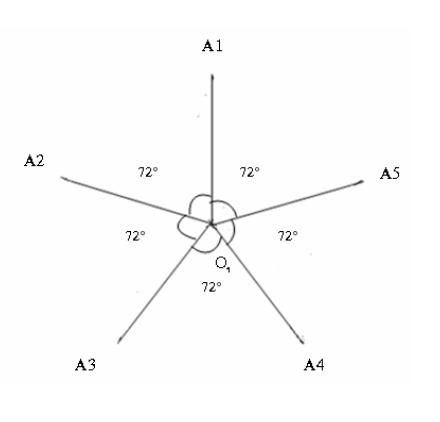
+ Cách xác định đỉnh: Nhận thấy 1 ngôi sao có 5 đỉnh sẽ cách đều tâm, hai đỉnh kề nhau sẽ cách nhau một góc 72o. Vậy để xác định đỉnh, chúng ta chỉ cần chọn 1 điểm cách tâm 1 khoảng r, sau đó quay quanh tâm theo góc 72o ta sẽ được đỉnh tiếp theo.
+ Từ 5 đỉnh của ngôi sao, sử dụng thuật toán dda nối các điểm thành các đường thẳng tạo thành ngôi sao.
- Thuật toán
+ Bước 1: Xác định đỉnh của ngôi sao bằng công thức
x[i] = x *cos(i* 72o) – y *sin(y * 72o) + (y +r)sin(i * 72o) + x(1- cos(i*72o))
y[i] = x *sin(i* 72o) + y *cos(y * 72o) + (y +r)(1-cos(i * 72o)) + x*sin(i*72o)
+ Bước 2: Sử dụng thuật toán DDA nối các điểm: 1 và 3, 1 và 4, 2 và 3, 2 và 5, 3 và 5 Ta được hình sau:
- Cài đặt
void ngoisao(Graphics g, intxt, intyt, intr) {
floatx[] = newfloat[5], y[] = newfloat[5], grad = (float) ((72 * 3.14) / 180);
x[0] = xt;
y[0] = yt - r;
for (inti = 1; i < 5; i++) {
x[i] = (float) (x[0] * Math.cos(i * grad) - y[0] * Math.sin(i * grad) + yt * Math.sin(i * grad)
+ xt * (1 - Math.cos(i * grad)));
y[i] = (float) (x[0] * Math.sin(i * grad) + y[0] * Math.cos(i * grad) + yt * (1 - Math.cos(i * grad))
- xt * Math.sin(i * grad));
}
DDA(g, Math.round(x[0]), Math.round(y[0]), Math.round(x[2]), Math.round(y[2]));
DDA(g, Math.round(x[0]), Math.round(y[0]), Math.round(x[3]), Math.round(y[3]));
DDA(g, Math.round(x[1]), Math.round(y[1]), Math.round(x[3]), Math.round(y[3]));
DDA(g, Math.round(x[1]), Math.round(y[1]), Math.round(x[4]), Math.round(y[4]));
DDA(g, Math.round(x[2]), Math.round(y[2]), Math.round(x[4]), Math.round(y[4]));
}
2. Vẽ bông hoa 5 cánh
- Ý tưởng:
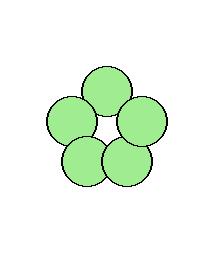
+ Bông hoa sẽ gồm 5 cánh là 5 hình tròn được xếp đều nhau quanh 1 hình tròn tâm
+ Cách xác định tâm của 5 cánh hoa: Tương tự như hình ngôi sao, ta nhận thấy 5 cánh sẽ cách đều tâm, nên sẽ có 5 tâm của mỗi cánh cách đều tâm chính, hai tâm kề nhau sẽ cách nhau một góc 72o. Vậy nên để xác định tâm, chúng ta chỉ cần chọn 1 điểm cách tâm 1 khoảng r (chúng ta có thể nâng khoảng r lên r +r /3 để các cánh hoa xa nhau hơn), sau đó quay quanh tâm theo góc 72o ta sẽ được cái đỉnh tiếp theo.
+ Sử dụng các thuật toán vẽ hình tròn, và tô màu để vẽ.
- Thuật toán:
+ Bước 1: Xác vị trí của cánh theo công thức:
x[i] = x *cos(i* 72o) – y *sin(y * 72o) + y sin(i * 72o) + x(1- cos(i*72o))
y[i] = x *sin(i* 72o) + y *cos(y * 72o) + y (1-cos(i * 72o)) + x*sin(i*72o)
+ Bước 2: Vẽ và tô màu các cánh
+ Bước 3: Vẽ và tô màu tâm vào giữa các cánh.
- Cài đặt
void veHoa(Graphics g, intxt, intyt, intr)
{
floatx[] = newfloat[5], y[] = newfloat[5], grad = (float) ((72 * 3.14) / 180);
x[0] = xt;
y[0] = yt - r;
r += r/3;
for (inti = 1; i < 5; i++) {
x[i] = (float) (x[0] * Math.cos(i * grad) - y[0] * Math.sin(i * grad) + yt * Math.sin(i * grad)
+ xt * (1 - Math.cos(i * grad)));
y[i] = (float) (x[0] * Math.sin(i * grad) + y[0] * Math.cos(i * grad) + yt * (1 - Math.cos(i * grad))
- xt * Math.sin(i * grad));
}
g.setColor(new Color(160, 236, 144));
for (inti = 0; i < 5; i++) {
g.setColor(new Color(160, 236, 144));
if (i == 1)
totron(g, (int) x[i], (int) y[i], r / 2);
else
totron(g, (int) x[i], (int) y[i], r / 2);
g.setColor(Color.black);
dtron(g, (int) x[i], (int) y[i], r / 2);
}
g.setColor(new Color(225, 208, 57));
totron(g, (int) xt, (int) yt, r / 2);
}
KẾT LUẬN
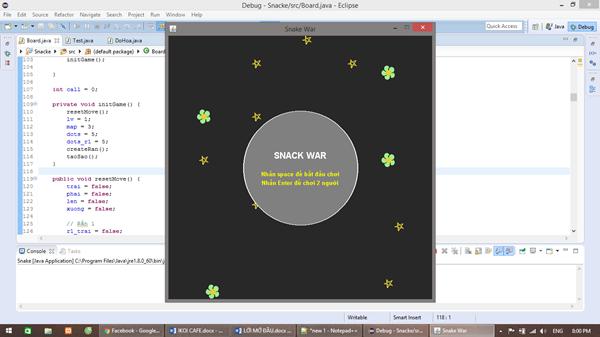
Trên nền tảng các thuật toán đồ họa cơ sở có thể áp dụng để vẽ các hình phức tạp hơn nhằm xây dựng ứng dụng cụ thể. Đây là một mảng hết sức thú vị và có rất nhiều ứng dụng, đặc biệt trong lĩnh vực giải trí. Với việc dùng các thuật toán vẽ đường thẳng, vẽ đường tròn, tô màu, vẽ ngôi sao, bông hoa tác giả đã xây dựng game “Snacke”.
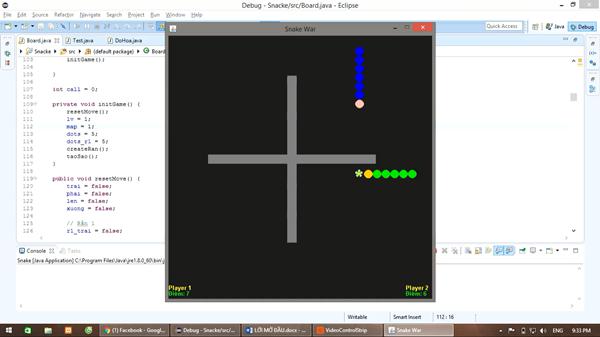
Giao diện chính
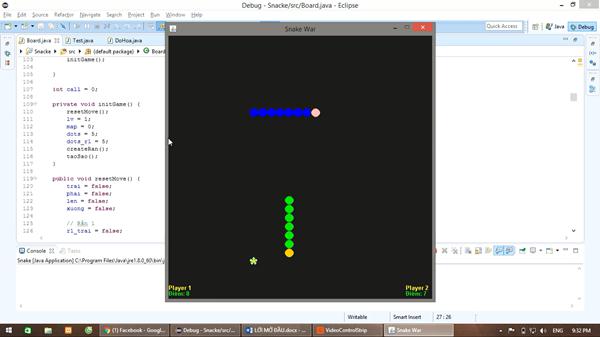
Màn chơi 1
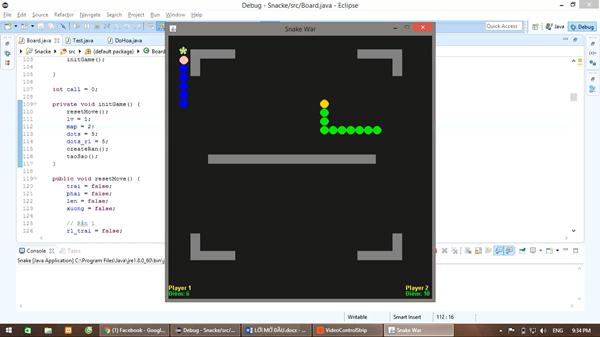
Màn chơi 2
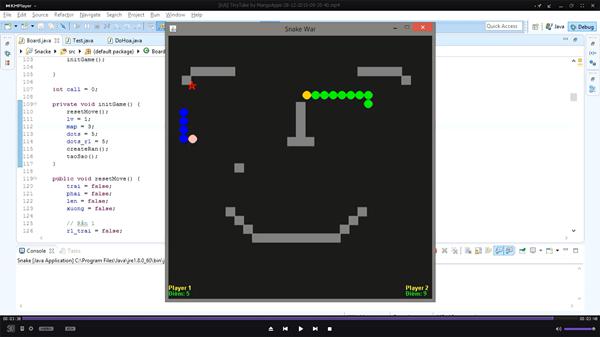
Màn chơi 4
Màn chơi 5
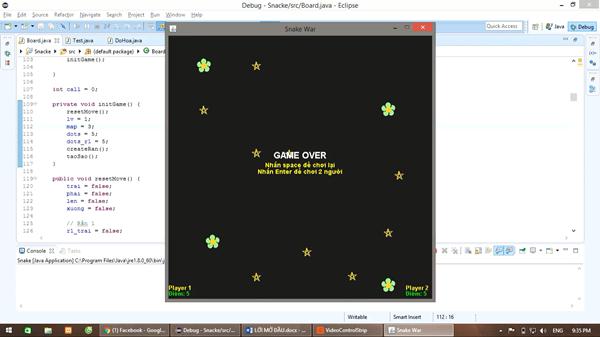
Kết thúc
TÀI LIỆU THAM KHẢO
[1]. Francis S. Hill, Computer Graphics, Macmillan Publishing Company, NewYork, 1990
[2]. James D.Foley, Andries Van Dam, Feiner, John Hughes, Computer Graphics - Principle and Practice, Addision Wesley, NewYork, 1996
[3]. Dương Anh Đức, Lê Đình Duy. Giáo trình Đồ họa máy tính, Trường Đại học Khoa học Tự nhiên, 1996
[4]. Lê Tấn Hùng- Huỳnh Quyết Thắng. Kỹ thuật đồ họa, NXB Khoa học và Kỹ thuật, Hà Nội 2004
PHỤ LỤC
- Cài đặt thuật toán DDA:
void DDA(Graphics g,int x1,int y1,int x2,int y2){
int dx, dy, step;
float y_inc, x_inc, x, y;
dx = x2 - x1;
dy = y2 - y1;
if(Math.abs(dx)> Math.abs(dy))
step = Math.abs(dx);
else
step = Math.abs(dy);
x_inc =(float) dx / step;
y_inc =(float) dy / step;
x = x1;
y = y1;
putpixel(g,(int) x,(int) y);
for(int k =1; k <= step; k++){
x = x + x_inc;
y = y + y_inc;
putpixel(g,(int) x,(int) y);
}
}
- Cài đặt thuật toán Bresenham vẽ đường tròn
privatevoid put8pixel(int xc,int yc,int x,int y)
{
putpixel(g, x + xc, y + yc);
putpixel(g,-x + xc, y + yc);
putpixel(g, x + xc,-y + yc);
putpixel(g,-x + xc,-y + yc);
putpixel(g, y + xc, x + yc);
putpixel(g,-y + xc, x + yc);
putpixel(g, y + xc,-x + yc);
putpixel(g,-y + xc,-x + yc);
}
privatevoid circle(int x0,int y0,int r)
{
int x =0;
int y = r;
int p =3-2* r;
while(x <= y)
{
put8pixel(x0,y0,x,y,15);
if(p <0)
{
p = p +4* x +6;
}
else
{
p = p +4*(x - y)+10;
y = y -1;
}
x = x +1;
}
}
- Tô hình vuông
+ Mục đích: Tạo chướng ngại vật trong trò chơi
+ Ý tưởng: Sử dụng thuật toán tô màu scanline để tô màu
+ Code:
void toVuong(Graphics g,intx, inty,intr){
for(inti=0;i<=r;i++){
DDA(g,x,y+i,x+r,y+i);
}
}
- Tô hình tròn
+ Mục đích: Vẽ intro game, vẽ hình nhân vật game, vẽ bông hoa
+ Ý tưởng: Sử dụng thuật toán scanline để tô màu
+ Code
void totron(Graphics g, intxc, intyc, intr) {
intr2=r-1;
while(r2>0){
dtron(g,xc,yc,r2);
r2--;
}
}
Tin mới
- ĐOÀN GIẢNG VIÊN TRƯỜNG ĐẠI HỌC HÀ TĨNH HÀNH HƯƠNG TỚI CÁC ĐỊA CHỈ ĐỎ - 08/04/2016 14:38
- KẾT THÚC THÀNH CÔNG “GIẢI BÓNG ĐÁ NAM SINH VIÊN KHOA KỸ THUẬT – CÔNG NGHỆ 2016” - 15/03/2016 01:57
- ẤN TƯỢNG NHỮNG TRẬN ĐẤU NGÀY KHAI MẠC – GIẢI BÓNG ĐÁ NAM SINH VIÊN KHOA KT-CN 2016 - 09/03/2016 02:04
- “IT –Đồng hành cùng mùa thực tập 2016” - 02/03/2016 06:58
- Trung tâm Kiểm định chất lượng công trình xây dựng Hà Tĩnh – Địa chỉ tin cậy của sinh viên ngành xây dựng Trường Đại học Hà Tĩnh - 21/02/2016 12:27
Các tin khác
- LCĐ Khoa Kỹ thuật-Công nghệ kiện toàn nhân sự ban chấp hành - 21/01/2016 15:01
- Điều cần có ở một kỹ sư xây dựng để tự tin bước vào nghề - 20/01/2016 15:26
- Tính năng mới của phần mềm Teamviewer - 20/01/2016 15:14
- Hội kết cấu và Công nghệ xây dựng Việt Nam tổ chức Đại hội Toàn quốc lần thứ VII (nhiệm kỳ 2015-2020) - 16/12/2015 13:48
- Nâng cao chất lượng công tác phục vụ hoạt động tự học, tự nghiên cứu của sinh viên tại thư viện Trường Đại học Hà Tĩnh - 09/12/2015 08:09